Лабораторная работа №3

Методы поиска

1. Цель работы

Цель данной работы:

1. изучить различные методы поиска.
2. программно реализовать хранение множества однотипных элементов и операции, перечисленные в индивидуальном задании так, чтобы они удовлетворяли требованиям, предъявляемым к сложности операций.

2. Краткие сведения из теории

В этой и нескольких последующих лабораторных работах будут рассматриваться способы хранения множества однотипных элементов. Основными критериями сравнения этих способов будут временные сложности алгоритмов поиска/добавления/удаления элементов множества. Главная задача авторов – показать различные способы организации хранения множества однотипных элементов. Также хотелось бы, чтобы читатель почувствовал взаимную зависимость способов хранения данных и сложности алгоритмов их обработки, понял важность изначального выбора структуры данных и алгоритмов их обработки, удовлетворяющей всем необходимым требованиям, следующим из особенностей эксплуатации программного продукта.

Хоть эта глава и называется «методы поиска» интерес представляют и операции добавления и удаления элементов. Эти операции представляют интерес, так как в реальных задачах редко встречается статическое множество, то есть множество, которое не меняется. Далее будет видно, как сильно зависят друг от друга способ хранения множества элементов и сложности перечисленных операций.

Начнем рассмотрение способов хранения множества однотипных элементов с точки зрения алгоритмов поиска/добавления/удаления с алгоритма линейного поиска.

2.1. Линейный (последовательный) поиск

Линейный поиск – самый простой из известных. Суть его заключается в следующем. Множество элементов просматривается последовательно в некотором порядке, гарантирующем, что будут просмотрены все элементы множества (например, слева направо). Если в ходе просмотра множества будет найден искомый элемент, просмотр прекращается с положительным результатом; если же будет просмотрено все множество, а элемент не будет найден, алгоритм должен выдать отрицательный результат. Именно так поступает человек, когда ищет что-то в неупорядоченном множестве. Например, при поиске нужной визитки в некотором неупорядоченном множестве визиток человек просто перебирает все визитки в поисках нужной.

Оформим описанный алгоритм в виде кусочка программы на Паскале. Пусть множество хранится в первых n элементах массива A. При этом не важен тип элементов множества, важна лишь возможность проверки эквивалентности элемента множества искомому элементу Key.

i := 1;
while (i<=n)and(A[i]<>Key) do Inc(i);
if A[i]=Key then <элемент найден> else <элемент не найден>;

В среднем этот алгоритм требует n/2 итераций цикла. Это означает сложность алгоритма поиска T(n). Единственное требование к способу хранения множества – существование некоторого порядка на множестве: чтобы можно было указать, что один элемент предшествует другому. Здесь можно хранить множество как в массиве (рассмотренный выше кусок программы), так и в обычном однонаправленном списке:

Type
  PListItem = ^TListItem;
  TListItem = record
    Item: TItem;
    Next: PListItem;
  end;

Рассмотрим добавление элемента Key во множество, хранимое в виде массива. Здесь достаточно просто дописать новый элемент в «конец» множества:

Inc(n); A[n] := Key;

Удалению элемента всегда предшествует успешный поиск. Это значит, что сложность операции удаления не может быть меньше сложности операции поиска. В данном случае при удалении нам придется сначала найти положение удаляемого элемента, затем все элементы, следующие за ним, сдвинуть на одну позицию к началу массива и уменьшить n. То есть в любом случае надо пробежать весь массив от начала до конца (это означает сложность T(n)):

i := 1;
while (i<=n)and(A[i]<>Key) do Inc(i); {поиск}
if A[i]=Key then
begin
  while i<n do
  begin
    A[i] := A[i+1]; {сдвигаем}
    Inc(i);
  end;
  Dec(n);
end;

Теперь положим, что множество хранится в виде списка. Добавление элемента сведется к добавлению элемента в начало списка (при добавлении в конец списка пришлось бы сначала искать конец, либо специально хранить указатель на последний элемент списка). Удаление элемента будет состоять из поиска и собственно удаления (никаких сдвигов последующих элементов производить не придется.).

2.2. Быстрый последовательный список

Этот метод поиска является небольшим усовершенствованием предыдущего. В любой программе, имеющей циклы, наибольший интерес представляет оптимизация именно циклов, то есть сокращение числа действий в них. Посмотрим на алгоритм линейного поиска (программу раздела 2.1.). В цикле while производится два сравнения: (i<=n) и (A[i]<>Key). Избавимся от одного из них (от первого), положив A[n+1] := Key. Тогда программа поиска будет выглядеть так:

A[n+1] := Key;
i := 1;
while A[i]<>Key do Inc(i);
if i<=n then <элемент найден> else <элемент не найден>;

Надо сказать, что хотя такой фрагмент кода будет работать быстрее, но его теоретическая сложность остается такой же – T(n). Гораздо больший интерес представляют методы, не только работающие быстро, но и дающие лучшую теоретическую сложность. Один из таких методов – дихотомический поиск.

2.3. Дихотомический (бинарный) поиск

Этот метод поиска предполагает, что множество хранится, как некоторая отсортированная (например, по возрастанию) последовательность элементов, к которым можно получить прямой доступ посредством индекса. Фактически речь идет о том, что множество хранится в массиве и этот массив отсортирован.

Суть метода заключается в следующем. Областью поиска (l, r) назовем часть массива с индексами от l до r, в которой предположительно находится искомый элемент. Сначала областью поиска будет часть массива (l, r), где l=1, а r=n, то есть вся заполненная элементами множества часть массива. Теперь найдем индекс среднего элемента m=(l+r) div 2. Если Key>A[m], то можно утверждать (поскольку массив отсортирован), что если Key есть в массиве, то он находится в одном из элементов с индексами от m+l до r, следовательно, можно присвоить l=m+1, сократив область поиска. В противном случае можно положить r=m. На этом заканчивается первый шаг метода. Остальные шаги аналогичны.

На каждом шаге метода область поиска будет сокращаться вдвое. Как только l станет равно r, то есть область поиска сократится до одного элемента, можно будет проверить этот элемент на равенство искомому и сделать вывод о результате поиска.

Запишем все сказанное в виде программы:

l := 1; r := n;
while (l<>r) do
begin
  m := (l+r) div 2;
  if Key>A[m] then l := m+1 else r := m;
end;
if A[l]=Key then <элемент найден> else <элемент не найден>;

Как уже было сказано, область поиска на каждом шаге сокращается вдвое, а это означает сложность T(log(n)).

Особого внимания здесь заслуживают операции добавления и удаления. Они должны сохранять массив отсортированным (лучше написать операции так, чтобы они не нарушали отсортированности массива, чем каждый раз сортировать его). Рассмотрим сначала добавление.

Чтобы при добавлении массив остался отсортированным, новый элемент должен быть вставлен в массив так, чтобы ему предшествовали меньшие элементы, а за ним следовали большие. То есть элементы, стоящие в месте вставки и за ним до конца массива должны быть сдвинуты на одну позицию в сторону конца массива:

i := n;
while (i>=1)and(A[i]>Key) do
begin
  A[i+1] := A[i]; {сдвигаем}
  Dec(i);
end;
A[i+1] := Key;
Inc(n);

Такая операция добавления имеет сложность T(n).

Удаление в том виде, в каком оно записано в разделе 2.1. сохраняет массив отсортированным.

2.4. Интерполяционный поиск

Рассмотрим еще один метод, имеющий хорошую теоретическую сложность. Как и предыдущий, этот метод предполагает, что множество хранится в массиве и массив отсортирован. Как и предыдущий метод, этот на каждом шаге своей работы сокращает область поиска. Но в отличие от предыдущего метода проба берется не в середине рассматриваемой области.

Пусть имеется область поиска (l, r). Предположим, что элементы множества – целые числа, возрастающие в арифметической прогрессии. Тогда искомый элемент должен находится в массиве (если он вообще там есть) под индексом

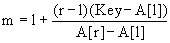(Это следует из свойств арифметической прогрессии)

В этом элементе и будем брать пробу.

l := 1; r := n;
while (l<>r) do
begin
  m := l+(r-l)*(Key-A[l])/(A[r]-A[l]);
  if Key>A[m] then l := m+1 else r := m;
end;
if A[l]=Key then <элемент найден> else <элемент не найден>;

Мы сделали очень большое допущение, предположив, что элементы массива представляют собой возрастающую арифметическую прогрессию. В реальности такая ситуация встречается редко. Но этот метод хорошо работает для любых пусть не идеально, но более-менее равномерно распределенных данных. Если же мы имеем дело с неравномерно распределенными данными, то интерполяционный поиск может увеличить число шагов по сравнению с дихотомическим поиском. Теоретическая сложность интерполяционного поиска – T(log(log(n))). Это, конечно, лучше, чем сложность дихотомического поиска, но эти преимущества становятся достаточно заметными лишь при очень больших значениях n. Практически на всех реальных n разница между дихотомическим и интерполяционным поиском по скорости не существенна.

Добавление и удаление можно реализовать так же, как при дихотомическом поиске. К этим операциям предъявляется то же требование: они должны сохранять массива отсортированным.

2.5. Сравнение рассмотренных методов

Приведенная табличка поможет сравнить методы друг с другом.

Быстрый последовательный поиск с хранением множества в списке (при списковом хранении удаление будет выполняться в среднем в 2 раза быстрее) лучше применять в случаях, когда операции добавления/удаления будут выполняться чаще операции поиска. В этом случае лучше проиграть на поиске, но выиграть на добавлении и удалении.

Для случая же когда будут преобладать операции поиска, лучшим выбором является дихотомический поиск. Почему не интерполяционный? Частично об этом уже сказано в разделе 2.4. Интерполяционный поиск предполагает, что данные распределены равномерно. В противном случае, возможно, замедление работы по сравнению с дихотомическим поиском. Да и дихотомический поиск работает достаточно быстро. Чтобы найти искомый элемент (или выяснить, что его нет) среди 1 млрд. элементов отсортированного множества, бинарному поиску хватит около 30 сравнений.

3. Контрольные вопросы

1. Почему последний из разобранных методов поиска называется интерполяционным?
2. Почему при хранении в списке невозможно воспользоваться дихотомическим и интерполяционным поиском?
3. Почему операция удаления при хранении множества в списке в среднем в 2 раза медленнее, чем при хранении в неотсортированном массиве?

4. Методические указания

В рассматриваемых задачах надо будет реализовать способ хранения множества однотипных значений таким образом, чтобы удовлетворить требования по сложности операций обработки множества и обосновать, почему получаются именно такие сложности операций.

Перед выполнением индивидуального задания ознакомиться со способами хранения множества элементов в массиве и методами поиска.

При выполнении индивидуального задания придерживаться следующей последовательности действий:

1. изучить словесную постановку задачи;
2. выбрать способ хранения множества элементов и метод поиска, который лучше всего подходит для решения поставленной задачи;
3. доказать, что для всех операций гарантируется требуемая в постановке задачи сложность.
4. разработать программу, решающую поставленную задачу;
5. оттестировать и отладить программу;
6. написать и представить к защите отчет по работе.

5. Содержание отчета

1. Титульный лист.
2. Словесная постановка задачи.
3. Алгоритм решения задачи в текстуальном виде.
4. Обоснование правильности выбора способа хранения множества однотипных элементов и метода поиска, исходя из постановки задачи. Доказательство того, что для всех операций гарантируется требуемая в постановке задачи сложность.
5. Листинг программы.
6. Ответы на контрольные вопросы по согласованию с преподавателем.

6. Варианты индивидуальных заданий

Задача 1. Используя память, пропорциональную n, хранить подмножества множества {1..n}.

Указание. Хранить множество как A: array [1..n] of boolean, где A[i]=true, если i принадлежит множеству.

Задача 2. Условия те же, что в задаче 1, но проверка пустоты должна требовать T(1) действий.

Указание. Действуем как в задаче 1. Дополнительно храним число элементов множества.

Задача 3. Используя память, пропорциональную n, хранить подмножества множества {1..n}.

Указание. Действуем как в предыдущей задаче, дополнительно храня минимальный элемент множества.

Задача 4. Используя память, пропорциональную n, хранить подмножества множества {1..n}.

Указание. Хранить множество как A: array [1..n] of boolean, где A[i]=true, если i принадлежит множеству. Дополнительно храним минимальный элемент, а для каждого — следующий и предыдущий по величине.

Задача 5. Число элементов множества не превосходит n. Элементами множества являются произвольные целые числа. Используя память, пропорциональную n, организовать такое хранение множества, что

Указание. Представим множество в виде двух переменных: A: array [1..n] of integer; Count: 0..n. Множество содержит Count элементов A[1], A[2], … , A[Count] и все они различны. По существу, множество будет храниться в стеке с произвольным доступом (чтение возможно не только из вершины стека).

Задача 6. Число элементов множества не превосходит n. Элементами множества являются произвольные целые числа. Используя память, пропорциональную n, организовать такое хранение множества, что

Указание. Действуем как в предыдущей задаче, но каждая операция должна сохранять упорядоченность массива, а при проверке принадлежности следует использовать дихотомический поиск.

Задача 7. Организовать массив данных [1..1000], значения элементов которого лежат в диапазоне от 50 000 000 до 100 000 000, так, чтобы экономно использовать память.

Указание. Создать массив, значения элементов которого лежат в диапазоне от 0 до 100.