РАЙОННАЯ (ГОРОДСКАЯ) ОЛИМПИАДА
ПО ИНФОРМАТИКЕ (1996-й год)
В 1996 году городские и районные олимпиады по информатике состоялись 14 декабря. Как обычно, они были проведены по единым заданиям, без учёта классов, что обусловлено практикой проведения последующих этапов олимпиады по информатике. Тексты задач составляются, в основном, в расчёте на учащихся 11-х классов, т.е. уровень сложности предлагаемых заданий предполагает знания учащихся по математике в объёме 10-11-го классов и знание какого-либо языка программирования в объёме школьного курса информатики. Однако это не означает, что в олимпиаде могут принимать участие только учащиеся 11-х классов. К участию в олимпиаде могут быть допущены учащиеся любых классов, если они увлекаются информатикой и имеют достаточную подготовку. Районный (городской) этап олимпиады предусматривает проведение только одного - теоретического - тура. Впрочем, в случае затруднений с распределением призовых мест и при наличии достаточного количества компьютеров возможно проведение дополнительного - практического - тура.
Задача1
Заданы четыре слова из десяти букв. Проверить, совпадают ли последняя буква первого слова с первой буквой второго, последняя буква второго слова с первой буквой третьего, последняя буква третьего слова с первой буквой четвёртого и последняя буква четвёртого слова с первой буквой первого. Если все эти буквы совпадают, то поместить буквы первого слова в первую строку матрицы размером 10*10, буквы второго слова - в последний столбец, буквы третьего слова в обратном порядке - в последнюю строку, буквы четвёртого слова в обратном порядке - в первый столбец. Если хотя бы одно совпадение букв не выполнено, то поместить буквы первых двух слов на место диагональных элементов матрицы.
(8 баллов)
Решение. Алгоритм достаточно очевиден и пояснений, на наш взгляд, не требует. По традиции, одна из задач районной олимпиады по сложности не превосходит обычного школьного уровня. На олимпиаде 1996 года это была задача 1.
Реализация на языке BASIC
10 DIM T$(10,10),A$(4)
20 FOR I=1 TO 4
30 PRINT I;"-е слово из десяти букв";
40 INPUT A$(I)
50 IF LEN(A$(I))<>10 THEN 30
60 NEXT I
70 FOR I=1 TO 10
80 FOR J=1 TO 10
90 T$(I,J)=" "
100 NEXT J,I
110 IF MID$(A$(1),10,1)=MID$(A$(2),1,1) AND MID$(A$(2),10,1)=MID$(A$(3),1,1) AND MID$(A$(3),10,1)=MID$(A$(4),1,1) AND MID$(A$(4),10,1)=MID$(A$(1),1,1) THEN GOSUB 130 ELSE GOSUB 190
120 END
130 ў заполнение матрицы (первый вариант)
140 FOR I=1 TO 9
150 T$(1,I)=MID$(A$(1),I,1): T$(I,10)=MID$(A$(2),I,1)
160 T$(10,10-I+1)=MID$(A$(3),I,1): T$(10-I+1,1)=MID$(A$(4),I,1)
170 NEXT I
180 RETURN
190 ў заполнение матрицы (второй вариант)
200 FOR I=1 TO 10
210 T$(I,I)=MID$(A$(1),I,1)
220 T$(10-I+1,I)=MID$(A$(2),I,1)
230 NEXT I
240 RETURN
Реализация на языке PASCAL
Var
S: array[1..4] of String[11];{длина на 1 больше, чтобы
можно было зафиксировать превышение длины при вводе}
Matr: array[1..10, 1..10] of Char;
i, j: Integer;
begin
for i := 1 to 4 do
begin
repeat
Write('Введите строку ', i, ':'); ReadLn(S[i]);
if Length(S[i])<>10 then
WriteLn('Строка должна быть длиной 10 символов.');
until Length(S[i])=10;
end;
for i := 1 to 10 do
for j := 1 to 10 do
Matr[i, j] := ' ';
if S[1,10]=S[2,1])and(S[2,10]=S[3,1])and
(S[3,10]=S[4,1])and(S[4,10]=S[1,1]) then
for i := 1 to 9 do
begin
Matr[1, i] := S[1, i]; Matr[i, 10] := S[2, i];
Matr[10, 11-i] := S[3, i]; Matr[11-i, 1] := S[4, i];
end else
for i := 1 to 10 do
begin
Matr[i, i] := S[1, i]; Matr[i, 11-i] := S[2, i];
end;
WriteLn('Искомая матрица:');
for i := 1 to 10 do
begin
for j := 1 to 10 do
Write(Matr[i, j]);
WriteLn;
end;
end.
Задача 2
Путник, перемещаясь из пункта A в пункт B, всегда видит перед собой часть пути и может заблаговременно решить, можно ли двигаться по прямой или придётся огибать какое-то препятствие. Компьютер, управляющий движением какого-либо объекта, тоже должен уметь "видеть", т.е. анализировать данные о расположении возможных препятствий и положении начальной и конечной точек маршрута.
Итак, на плоскости заданы четыре точки A, B, C, D, не лежащие на одной прямой. Отрезок CD - "стена", через которую невозможно ни перелезть, ни перепрыгнуть. Требуется написать программу, проверяющую, можно ли, перемещаясь из точки A в точку В, двигаться по прямой или придется обходить стену.
(16 баллов)
Решение. Фактически в задаче требуется разработать алгоритм, позволяющий определить, пересекаются ли два отрезка, заданные координатами своих концов. Для ответа на этот вопрос вовсе не нужно искать точку пересечения отрезков. Достаточно понять, что отрезки M1M2 и M3M4 не имеют общей точки (ни внутренней, ни граничной), только если выполняется хотя бы одно из условий:
- точки M3 и M4 лежат в одной полуплоскости относительно прямой, проходящей через отрезок M1M2, но не на прямой;
- точки M1 и M2 лежат в одной полуплоскости относительно прямой, проходящей через отрезок M3M4, но не на прямой.
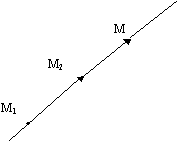
Разработаем схему проверки этих условий. Рассмотрим прямую, проходящую через точки M1(x1,y1) и M2(x2,y2), и некоторую точку M(x,y). Точка M принадлежит прямой M1M2 тогда и только тогда, когда вектор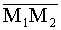 
=(x2-x1,y2-y1) коллинеарен вектору 
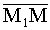=(x-x1,y-y1), т.е. когда координаты этих векторов пропорциональны: 
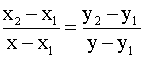. Преобразовав полученное соотношение к более удобному для проверки на компьютере виду, получаем, что прямой, проходящей через точки (x1,y1) и (x2,y2), принадлежат те и только точки (x,y), чьи координаты удовлетворяют условию (x-x1)(y2-y1)-(x2-x1)(y-y1)=0.
Обозначим F(x,y)=(x-x1)(y2-y1)-(x2-x1)(y-y1). Прямая M1M2 разбивает координатную плоскость на две полуплоскости, причём для всех точек одной полуплоскости F(x,y)>0, а для всех точек другой полуплоскости F(x,y)<0. Таким образом, точки (x3,y3) и (x4,y4) лежат в одной полуплоскости относительно данной прямой (но не на самой прямой) в том и только том случае, когда справедливо соотношение F(x3,y3)*F(x4,y4)>0. В алгоритме, который позволяет определить, пересекаются ли два отрезка, это условие проверяется дважды: сначала для прямой, по которой должен проходить маршрут, и концов стены, затем для прямой, на которой стоит стена и начальной и конечной точек пути. Сообщение "Надо обходить стену" выводится только, если обе проверки дали отрицательный результат.
Реализация на языке BASIC
10 INPUT "Координаты начальной и конечной точек пути"; X1,Y1,X2,Y2
20 INPUT "Координаты концов стены"; X3,Y3,X4,Y4
30 DEF FNF(X,Y)=(X-X1)*(Y2-Y1)-(Y-Y1)*(X2-X1)
40 D=FNF(X3,Y3):D1=FNF(X4,Y4)
50 IF D=0 AND D1=0 THEN PRINT "Точки лежат на одной прямой. Повторите ввод": GOTO 10
60 IF D*D1>0 THEN PRINT "Можно идти по прямой": GOTO 110
70 DEF FNG(X,Y)=(X-X3)*(Y4-Y3)-(Y-Y3)*(X4-X3)
80 D=FNG(X1,Y1):D1=FNG(X2,Y2)
85 IF D*D1=0 THEN PRINT "Начальная или конечная точка
пути оказалась на стене. Задача не имеет смысла":
GOTO 110
90 IF D*D1>0 THEN PRINT "Можно идти по прямой": GOTO 110
100 PRINT "Надо обходить стену"
110 END
Реализация на языке PASCAL
Var
X1, Y1, X2, Y2, X3, Y3, X4, Y4, D, D1: Real;
function F(X, Y, X1, Y1, X2, Y2: Real): Real;
begin
F := (X-X1)*(Y2-Y1)-(Y-Y1)*(X2-X1);
end;
begin
repeat
Write('Введите координаты начальной и конечной '+
'точек пути:');
ReadLn(X1, Y1, X2, Y2);
Write('Введите координаты концов стены:');
ReadLn(X3, Y3, X4, Y4);
D := F(X3, Y3, X1, Y1, X2, Y2);
D1 := F(X4, Y4, X1, Y1, X2, Y2);
if (D=0)and(D1=0) then
WriteLn('Точки лежат на одной прямой. Повторите.');
until (D<>0)or(D1<>0);
if D*D1>0 then
WriteLn('Можно идти по прямой.')
else
begin
D := F(X1, Y1, X3, Y3, X4, Y4);
D1 := F(X2, Y2, X3, Y3, X4, Y4);
if D*D1=0 then
WriteLn('Начальная или конечная точка пути'+
'на стене.')
else
if D*D1>0 then
WriteLn('Можно идти по прямой.')
else
WriteLn('Надо обходить стену.');
end;
end.
Задача 3
В настоящее время очень популярно использование электронных средств для шифровки и дешифровки секретных сообщений. Составить программу, реализующую шифровку по методу Гронсфельда сообщения, содержащего только русские строчные буквы и знаки препинания.
В этом методе используется "ключ" - конечная последовательность цифр, которую записывают подряд над текстом, требующим шифровки, пропуская знаки препинания и пробелы. При шифровке каждая буква текста заменяется на букву, которая в алфавите смещена относительно данной на расстояние, указываемое цифрой, написанной над данной буквой. При этом считается, что после буквы "я" следует снова "а", "б", "в" и т.д. Например, если в качестве ключа выбрана последовательность 732513, то получается:
732513732 51373251 37325 1373251
настоящий виновник кражи алмазов - исходный текст
фгучпвалл зйрхепнл нчгин боугйуг - шифровка
(16 баллов)
Решение. В данной задаче затруднения, которые могли бы возникнуть, носят чисто технический характер, так как выполнить вручную описанные в задаче действия не составляет никакого труда.
Следует обратить внимание, что замене (шифровке) подлежат только символы русского алфавита, поэтому при организации посимвольного просмотра шифруемого текста надо позаботиться, чтобы были пропущены без замены знаки препинания. В реализациях алгоритма шифровки на языках программирования используются вспомогательные строковые величины, предназначенные для передачи программе информации о допустимых символах текста: строчных символах русского алфавита (шифруемые символы) и знаках препинания (не шифруемые символы).
Реализация на языке BASIC
10 C$="абвгдежзийклмнопрстуфхцчшщъыьэюя"
20 D$=";,.?!- ()"
30 PRINT "Шифруемый текст должен содержать только"
40 PRINT "русские строчные буквы и знаки препинания"
50 INPUT "Введите текст"; A$
60 INPUT "Введите ключ (последовательность цифр)"; B$
70 FOR I=1 TO LEN(B$)
80 IF MID$(B$,I,1)<"0" OR MID$(B$,I,1)>"9" THEN PRINT "Ключ содержит недопустимые символы": GOTO 60
90 NEXT I
100 N=1
110 FOR I=1 TO LEN(A$)
120 S$=MID$(A$,I,1)
125 K=INSTR(C$,S$):L=INSTR(D$,S$)
130 IF K=0 AND L=0 THEN PRINT "Текст содержит недопустимые символы": GOTO 170
140 IF K<>0 THEN GOSUB 180
150 NEXT I
160 PRINT A$
170 END
180 'шифровка
190 M=VAL(MID$(B$,N,1))
200 IF K+M<=32 THEN K=K+M ELSE K=K+M-32
210 MID$(A$,I,1)=MID$(C$,K,1)
220 IF N<LEN(B$) THEN N=N+1 ELSE N=1
230 RETURN
Реализация на языке PASCAL
const
Letters: String='абвгдежзийклмнопрстуфхцчшщьыъэюя';
SetLetters=['а', 'б', 'в', 'г', 'д', 'е', 'ж', 'з',
'и', 'й', 'к', 'л', 'м', 'н', 'о', 'п', 'р', 'с',
'т', 'у', 'ф', 'х', 'ц', 'ч', 'ш', 'щ', 'ь', 'ы',
'ъ', 'э', 'ю', 'я'];
SetSigns=[';', ',', '.', '?', '!', '(', ')', '-', ' '];
Var
Flag: Boolean;
S, Key: String;
i, j, k: Integer;
begin
WriteLn('Шифруемый текст должен содержать только '+
'русские строчные буквы и знаки препинания.');
repeat
Write('Введите текст:'); ReadLn(S);
Flag := True;
for i := 1 to Length(S) do
if not (S[i] in SetLetters+SetSigns) then
begin
Flag := False;
Break;
end;
if not Flag then
WriteLn('Неверный ввод. Повторите.');
until Flag;
repeat
Write('Введите ключ:'); ReadLn(Key);
Flag := True;
for i := 1 to Length(Key) do
if not (Key[i] in ['0'..'9']) then
begin
Flag := False;
Break;
end;
if not Flag then
WriteLn('Неверный ввод. Повторите.');
until Flag;
j := 1;
for i := 1 to Length(S) do
if S[i] in SetLetters then
begin
k := Pos(S[i], Letters)+Ord(Key[j])-Ord('0');
if k>32 then k := k-32;
S[i] := Letters[k];
if j=Length(Key) then j := 1 else Inc(j);
end;
WriteLn('Зашифрованый текст: ', S);
end.
Задача 4
Составить алгоритм, который для заданного натурального числа находит наименьшее из бульших чисел, составленных из тех же цифр.
(24 балла)
Решение. Понятно, что искомое число получается некоторой перестановкой цифр исходного числа, причём так как требуется получить наименьшее из бульших чисел, то перестановка должна затрагивать самые младшие из тех разрядов, перестановки в которых позволяют получать бульшие числа.
Просматриваем цифры исходного числа справа налево (младшие разряды!) в поисках такой пары соседних цифр, чтобы цифра, стоящая в числе левее, была меньше цифры, стоящей правее (в противном случае после перестановки этих цифр число не станет больше). Если такую пару цифр найти не удаётся, в исходном числе цифры упорядочены по убыванию, поэтому из цифр этого числа невозможно составить новое, которое было бы больше исходного.
Предположим теперь, что найдена пара цифр, удовлетворяющая сформулированному выше условию. Допустим, это цифры, стоящие в позициях i-1 и i. Тем самым определена позиция, начиная с которой будут переставлены цифры исходного числа. Прежде чем переставлять цифры в позициях i и i-1, надо проверить, не найдётся ли цифры, стоящей в числе правее, чем i-ая, которая была бы больше (i-1)-ой цифры, но меньше i-ой. Если этого не сделать, полученное после перестановки число может оказаться не наименьшим из возможных. Таким образом, цифра исходного числа, стоящая в позиции i-1, переставляется с наименьшей из цифр, стоящих в исходном числе правее и бульших, чем (i-1)-ая цифра. И наконец, цифры
числа, оказавшиеся после этой перестановки в позициях i и далее, упорядочиваются по возрастанию, чтобы в полученном числе большие цифры стояли в младших разрядах.
Реализация на языке BASIC
10 INPUT "Введите натуральное число"; N
20 IF N<>INT(N) OR N<=0 THEN 10
30 IF N<=9 THEN 200
40 N$=MID$(STR$(N),2): DIM C(LEN(N$))
50 FOR I=1 TO LEN(N$)
60 C(I)=VAL(MID$(N$,I,1))
70 NEXT I
80 FOR I=LEN(N$) TO 2 STEP -1
90 IF C(I-1)>=C(I) THEN 190
100 C(0)=C(I)
105 K=I
110 FOR J=I TO LEN(N$)
120 IF C(J)>C(I-1) AND C(J)<C(0) THEN C(0)=C(J): K=J
130 NEXT J
140 C(K)=C(I-1)
145 C(I-1)=C(0)
150 FOR J=I TO (LEN(N$)+I-1)/2
160 C(0)=C(J): C(J)=C(LEN(N$)-J+I): C(LEN(N$)-J+I)=C(0)
170 NEXT J
180 GOTO 210
190 NEXT I
200 PRINT "В данном случае не существует чисел, больших данного и состоящих из тех же цифр": GOTO 250
210 FOR I=1 TO LEN(N$)
220 PRINT MID$(STR$(C(I)),2);
230 NEXT I
240 PRINT
250 END
Реализация на языке PASCAL
Var
N: LongInt;
S: String;
i, j, k: Byte;
procedure Swap(X1, X2: Byte);
Var
T: Char;
begin
T := S[X1]; S[X1] := S[X2]; S[X2] := T
end;
begin
repeat
Write('Введите натуральное число:'); ReadLn(N);
if N<=0 then WriteLn('Неверный ввод. Повторите.');
until N>0;
Str(N, S); i := Length(S);
while (i>1)and(S[i-1]>=S[i]) do Dec(i);
if i=1 then
WriteLn('В данном случае не существует решения.')
else
begin
k := i;
for j := Length(S) downto i+1 do
if S[j]>=S[k] then Break
else
if S[j]>S[i-1] then k := j;
Swap(i-1, k);
for j := 1 to (Length(S)+1-i)div 2 do
Swap(i+j-1, Length(S)+1-j);
WriteLn('Искомое число: ', S);
end;
end.