Tree

Лабораторная работа №4

Сбалансированные деревья

1. Цель работы

2. Необходимое теоретическое введение

2.1. Двоичные деревья

Рассмотрим еще один способ хранения множества значений – представление множеств с помощью деревьев.

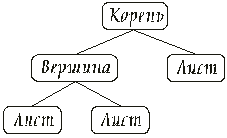
В дискретной математике дерево определяется как граф без циклов. В каждой вершине такого графа будем хранить значение некоторого типа T. Такое дерево назовем T-деревом. Фиксируем некоторую вершину и назовем ее корнем дерева. Соседние с ней вершины назовем сыновними и расположим чуть ниже. У этих вершин могут быть свои сыновние вершины. Вообще, у каждой вершины может быть несколько сыновей. Если вершина не имеет сыновей, то назовем ее листом.

У всякой вершины, кроме корня, должен быть единственный отец. Корень отца не имеет.

Двоичным назовем такое дерево, у которого каждая вершина может иметь не более двух сыновей.

Поддеревом назовем вершину со всеми ее потомками.

На первом уровне двоичного дерева может быть только одна вершина – корень, на втором – две (сыновья корня), на третьем – четыре (сыновья сыновей корня). В общем случае на i-м уровне может быть до 2^i-1 вершин. Дерево, содержащее n полностью заполненных уровней, будем называть полным. Полное двоичное дерево содержит 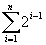=2ⁱ-1 вершин.

Всякое непустое двоичное T-дерево разбивается на 3 части: корень, левое и правое поддеревья. Отсюда можно дать следующее рекурсивное определение двоичного дерева:

пустое дерево – двоичное дерево;
вершина с левым и правым двоичными поддеревьями – двоичное дерево.

Левое и правое поддеревья могут быть пустыми.

Прямо из рекурсивного определения дерева можно вывести следующее ссылочное представление дерева в программе:

PTree = ^TTree;
TTree = record
  Item: T; {элемент дерева}
  Left, Right: PTree; {указатели на поддеревья}
end;

Где Left, Right равны nil, если соответствующие поддеревья пусты.

Есть еще нессылочный способ хранения деревьев. Пусть мы имеем дело с полным двоичным деревом, состоящим из n уровней. Можно организовать такое хранение дерева в массиве Value: array[1..N] of T, что:

Value[1] – корень дерева;

Value[2*i] – левый сын вершины Value[i];

Value[2*i+1] – правый сын вершины Value[i].

Недостаток такого хранения дерева – большие накладные расходы при изменении структуры дерева (например, если мы меняем местами два поддерева). Этот способ также неэкономен, если мы имеем дело с неполным двоичным деревом (в этом случае мы все равно вынуждены выделять память под все (даже отсутствующие) вершины полного двоичного дерева).

Высотой поддерева будем считать максимальную длину цепи y[1]..y[n] его вершин такую, что y[i+1] – сын y[i] для всех i. Высота пустого дерева равна 0. Высота дерева из одного корня – единице. Высота дерева на рисунке на предыдущей странице равна 3-м.

Обычные деревья не дают выигрыша при хранении множества значений. При поиске элемента мы все равно должны будем просмотреть все дерево. Однако можно организовать хранение элементов в дереве так, чтобы при поиске элемента достаточно было просмотреть лишь часть дерева. Для этого надо ввести следующее требование упорядоченности дерева:

Двоичное T-дерево упорядочено, если для любой вершины X справедливо такое свойство: все элементы, хранимые в левом поддереве, меньше элемента, хранимого в X, а все элементы, хранимые в правом поддереве, больше элемента, хранимого в X.

Важное свойство упорядоченного дерева: все элементы его различны.

В дальнейшем будет идти речь только о двоичных упорядоченных деревьях, опуская слова «двоичный» и «упорядоченный».

2.2. Поисе/добавление/удаление в T-деревьях

Алгоритм поиска можно записать, пользуясь рекурсивным определением двоичного дерева в рекурсивном виде. Если искомый элемент Item меньше Tree^.Item, то поиск продолжается в левом поддереве, если равен – то поиск считается успешным, если больше – поиск продолжается в правом поддереве; поиск считается неудачным, если мы дошли до пустого поддерева, а элемент найден не был:

function Exist(Item: T; Tree: PTree): Boolean;
begin
  if Tree=nil then
  begin
    Exist := False; 
    Exit
  end;
  if Tree^.Item=Item then
    Exist := True
  else
    if Tree^.Item>Item then
      Exist := Exist(Item, Tree^.Left)
    else
      Exist := Exist(Item, Tree^.Right);
end;

Можно написать аналогичную нерекурсивную программу, но мы здесь этого делать не будем. Скажем только, что нерекурсивная программа здесь уместнее. Она позволит избежать избыточного хранения информации. Каждый рекурсивный вызов размещает в стеке локальные переменные Item и Tree, а также адрес точки возврата из подпрограммы. В нерекурсивном варианте можно обойтись одной переменной Item и одной переменной Tree.

Как писать нерекурсивную программу обработки дерева, мы рассмотрим на примере алгоритма добавления элемента в дерево. Сначала надо найти вершину, к которой в качестве сына мы добавим новую вершину (фактически произвести поиск), а затем присоединить к найденной новую вершину, содержащую добавляемый элемент Item (процедура написана в предположении, что добавляемого элемента в дереве нет):

procedure Add(Item: T; Tree: PTree);
Var
  NewNode: PTree;
begin
  {поиск вершины}
  while ((Item>Tree^.Item)and(Tree^.Right<>nil))or
   ((Item<Tree^.Item)and(Tree^.Left<>nil)) do
    if Item>Tree^.Item then
      Tree := Tree^.Right
    else
      Tree := Tree^.Left;
  {создание и добавление новой вершины}
  NewNode := New(PTree);
  NewNode^.Item := Item; 
  NewNode^.Left := nil;
  NewNode^.Right := nil;
  If Item>Tree^.Item then
    Tree^.Right := NewNode
  else
    Tree^.Left := NewNode;
end;

Процедура удаления элемента будет несколько сложнее. При удалении может случиться, что удаляемый элемент находится не в листе, то есть вершина имеет ссылки на реально существующие поддеревья. Эти поддеревья терять нельзя, а присоединить два поддерева на одно освободившееся после удаления место невозможно. Поэтому надо поступать по другому. Надо поместить на освободившееся место либо самый правый элемент из левого поддерева, либо самый левый из правого поддерева. Нетрудно убедиться, что упорядоченность дерева при этом не нарушится. Договоримся, что мы будем заменять на самый левый элемент правого поддерева.

Надо не забыть, что при замене вершина, на которую мы будем производить замену, может иметь правое поддерево. Это поддерево надо поставить вместо перемещаемой вершины.

procedure Del(Item: T; Tree: PTree);
Var
  Tree2, Father: PTree;
  Dir: (L, R); {направление движения (влево/вправо)}
begin
  {поиск удаляемого элемента}
  Father := nil; {отец элемента}
  while ((Item>Tree^.Item)and(Tree^.Right<>nil))or
   ((Item<Tree^.Item)and(Tree^.Left<>nil)) do 
  begin
    Father := Tree;
    if Item>Tree^.Item then 
    begin
      Tree := Tree^.Right; Direction := R;
    end else 
    begin
      Tree := Tree^.Left; Direction := L;
    end;
  end;
  if (Tree^.Left<>nil)and(Tree^.Right<>nil then
  begin{требуется замена}
    Father := Tree; Tree2 := Tree^.Right;
    While (Tree2^.Left<>nil) do 
    begin
      Father := Tree2; Tree2 := Tree2^.Left;
    end;
    Tree^.Item := Tree2^.Item;
    Father^.Left := Tree2^.Right;
    Dispose(Tree2);
  end else
    {удаление}
    if (Tree^.Left=nil) then
    begin
      if Father<>nil then 
        if Direction=L then 
          Father^.Left := Tree^.Right;
        else
          Father^.Right := Tree^.Right;
      Dispose(Tree);
    end else
    begin 
      if Father<>nil then 
        if Direction=L then 
          Father^.Left := Tree^.Left;
        else
          Father^.Right := Tree^.Left;
      Dispose(Tree);
    end;
end;

Каковы же теоретические сложности этих алгоритмов (то, что они одинаковы, понятно, так как в основе везде поиск)? В лучшем случае – случае полного двоичного дерева – мы получим сложность T_max(log(n)). В худшем случае наше дерево может выродиться в список. Такое может произойти, например, при добавлении элементов в порядке возрастания. При работе со списком в среднем нам придется просмотреть половину списка. Это даст сложность T(n).

Итак, в худшем случае хранение в упорядоченном дереве никакого выигрыша по сравнению с обычным способом хранения множества в массиве не дает. В лучшем случае для всех операций (поиск/добавление/удаление) получается логарифмическая сложность, а это очень хорошо (ни один из рассмотренных ранее способов хранения такого результата для всех операций не давал). Но как гарантировать логарифмическую сложность всегда? Выход открывает способ, который был предложен в 1962 году двумя советскими математиками – Г.М.Адельсоном-Вельским и Е.М.Ландисом.

2.3. АВЛ-деревья

Так исторически сложилось, что у этих деревьев есть два альтернативных названия: АВЛ-деревья и сбалансированные деревья. АВЛ произошло от фамилий изобретателей. А почему сбалансированные, сейчас разберемся.

Идеально сбалансированным называется дерево, у которого для каждой вершины выполняется требование: число вершин в левом и правом поддеревьях различается не более, чем на 1. Однако идеальную сбалансированность довольно трудно поддерживать. В некоторых случаях при добавлении/удалении может потребоваться значительная перестройка дерева, не гарантирующая логарифмической сложности. Поэтому Г.М.Адельсон-Вельский и Е.М.Ландис ввели менее строгое определение сбалансированности и доказали, что при таком определении можно написать программы добавления/удаления, имеющие логарифмическую сложность и сохраняющие дерево сбалансированным.

Дерево считается сбалансированным по АВЛ (в дальнейшем просто «сбалансированным»), если для каждой вершины выполняется требование: высота левого и правого поддеревьев различаются не более, чем на 1. Не всякое сбалансированное дерево идеально сбалансировано, но всякое идеально сбалансированное дерево сбалансировано.

2.3.1. Вращения

При операциях добавления и удаления может произойти нарушение сбалансированности дерева. В этом случае потребуются некоторые преобразования, не нарушающие упорядоченности дерева и способствующие лучшей сбалансированности.

Рассмотрим такие преобразования.

Предварительно договоримся, что в каждой вершине дерева помимо значения элемента будем хранить показатель сбалансированности в данной вершине. Показатель сбалансированности - разница между высотами правого и левого поддеревьев.

PTree = ^TTree;
TTree = record
  Item: T; {элемент дерева}
  Left, Right: PTree; {указатели на поддеревья}
  Balance: ShortInt; {показатель сбалансированности}
end;

В сбалансированном дереве показатели сбалансированности всех вершин лежат в пределах от -1 до 1. При операциях добавления/удаления могут появляться вершины с показателями сбалансированности -2 и 2.

А теперь перейдем к рассмотрению преобразований.

2.3.1.1. Малое левое вращение

Пусть показатель сбалансированности вершины, в которой произошло нарушение баланса, равен -2, а показатель сбалансированности корня левого поддерева равен -1. Тогда восстановить сбалансированность такого поддерева можно следующим преобразованием, называемым малым левым вращением:

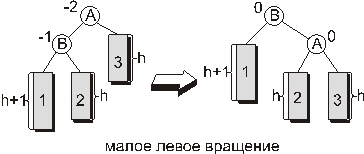
На приведенном рисунке прямоугольниками обозначены поддеревья. Рядом с поддеревьями указана их высота. Поддеревья помечены арабскими цифрами. Кружочками обозначены вершины. Цифра рядом с вершиной - показатель сбалансированности в данной вершине. Буква внутри кружка - условное обозначение вершины.

Как видно из рисунка после малого левого вращения показатель сбалансированности вершины, в которой было нарушение баланса, становится равным нулю.

2.3.1.2. Малое правое вращение

В случае, когда показатель сбалансированности вершины, в которой произошло нарушение баланса, равен 2, а показатель сбалансированности корня правого поддерева равен 1, восстановить сбалансированность в вершине можно с помощью преобразования, называемого малым правым вращением. Это вращение симметрично малому левому и схематично изображено на следующем рисунке:

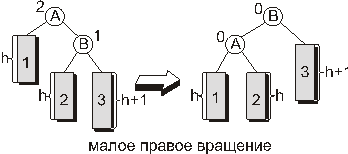
2.3.1.3. Большое левое вращение

Несколько сложнее случай, когда показатель сбалансированности в вершине, в которой произошло нарушение баланса равен -2, а показатель сбалансированности в корне левого поддерева равен 1 или 0. В этом случае применяется преобразование, называемое большим левым вращением. Как видно из рисунка здесь во вращении участвуют три вершины, а не две как в случае малых вращений.

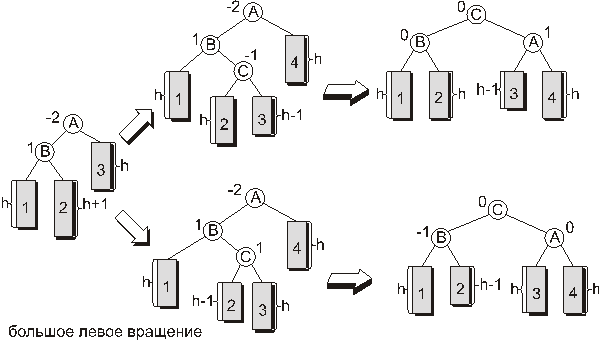
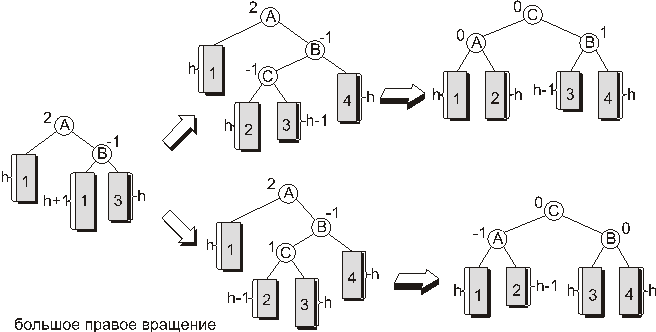
2.3.1.4. Большое правое вращение

Большое правое вращение применяется, когда показатель сбалансированности вершины, в которой произошло нарушение баланса, равен 2, а показатель сбалансированности корня правого поддерева равен -1 или 0. Большое правое вращение симметрично большому левому и схематично изображено на следующем рисунке:

2.3.2. Восстановление сбалансированности

Пусть имеется дерево, сбалансированное всюду, кроме корня, а в корне показатель сбалансированности по модулю равен 2-м. Такое дерево можно сбалансировать с помощью одного из четырех вращений. При этом высота дерева может уменьшиться на 1. Для восстановления баланса после удаления/добавления вершины надо пройти путь от места удаления/добавления до корня дерева, проводя при необходимости перебалансировку и изменение показателя сбалансированности вершин вдоль пути к корню. Можно доказать, что в других вершинах перебалансировка и изменение показателя сбалансированности не понадобятся.

2.3.3. Добавление элемента в сбалансированное дерево

Схематично алгоритм вставки нового элемента в сбалансированное дерево будет состоять из следующих трех основных шагов:

Поиск по дереву.
Вставка элемента в место, где закончился поиск, если элемент отсутствует.
Восстановление сбалансированности.

1-ый шаг необходим для того, чтобы убедиться в отсутствии элемента в дереве, а также найти такое место вставки, чтобы после вставки дерево осталось упорядоченным. Первые два шага ничем не отличаются от алгоритма, приведенного в разделе 2.2.

3-ий шаг представляет собой обратный проход по пути поиска: от места добавления к корню дерева. По мере продвижения по этому пути корректируются показатели сбалансированности проходимых вершин и производится балансировка там, где это необходимо. Добавление элемента в дерево никогда не требует более одного поворота.

2.3.4. Удаление элемента из сбалансированного дерева

Алгоритм удаления элемента из сбалансированного дерева будет выглядеть так:

Поиск по дереву.
Удаление элемента из дерева.
Восстановление сбалансированности дерева (обратный проход).

1-ый шаг необходим, чтобы найти в дереве вершину, которая должна быть удалена. Первых два шага аналогичны удалению элемента, приведенному в разделе 2.2.

3-ий шаг представляет собой обратный проход от места, из которого взят элемент для замены удаляемого, или от места, из которого удален элемент, если в замене не было необходимости.

Операция удаления может потребовать перебалансировки всех вершин вдоль обратного пути к корню дерева, то есть порядка log(N) вершин. Доказательство того, что порядок числа вершин имеет такой аналитический вид, смотрите в следующем разделе.

2.3.5. Анализ операций над сбалансированным деревом

Понятно, что в случае полного двоичного дерева (наилучший случай) мы получим сложность T(log(n)) (на каждом шаге размер дерева поиска будет сокращаться вдвое). Рассмотрим минимальное сбалансированное дерево (худший случай). Таким будет дерево, у которого для каждой вершины высота левого и правого поддеревьев различаются на 1. Для такого дерева можно записать следующую рекуррентную формулу для числа вершин (h – высота дерева):

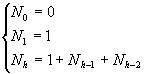
Покажем, что h<log₂(N_h). Для этого необходимо и достаточно показать, что 2^h>N_h. Докажем последнее методом математической индукции.

а) h=0: 2⁰>N₀=0;

б) h=1: 2¹>N₁=1;

в) h>1: Пусть 2^h-2>N_h-2 и 2^h-1>N_h-1.

Тогда 2^h-2+2^h-1>N_h-2+ N_h-1.

И далее получаем 2^h>1+2^h-2+2^h-1>1+N_h-2+ N_h-1=N_h, что и требовалось доказать.

Таким образом, мы доказали, что алгоритмы поиска/добавления/удаления элементов в сбалансированном дереве имеют сложность T(log(n)).

Г.М.Адельсон-Вельский и Е.М.Ландис доказали теорему, согласно которой высота сбалансированного дерева никогда не превысит высоту идеально сбалансированного дерева более, чем на 45%.

3. Контрольные вопросы

Что такое дерево, двоичное дерево, поддерево?
Приведите рекурсивное определение дерева, определение упорядоченного дерева.
Приведите два способа хранения деревьев в памяти ЭВМ, укажите их недостатки и достоинства.
Как надо изменить процедуру Add, чтобы она корректно работала в случае, если вершина в дереве уже есть? Пояснение: в этом случае значение в дерево заносить не надо.
Чем алгоритм удаления из упорядоченного дерева сложнее алгоритма добавления?
Приведите определение идеально сбалансированного дерева и дерева сбалансированного по АВЛ.
Что такое вращения и для чего они применяются? Перечислите используемые в этой работе вращения.
Что такое коэффициент сбалансированности и почему его следует хранить для каждой вершины дерева?
Перечислите три основных этапа алгоритма добавления в сбалансированное дерево.
Перечислите три основных этапа алгоритма удаления из сбалансированного дерева.

4. Методические указания

Перед выполнением индивидуального задания ознакомиться с тем, что такое дерево, упорядоченное дерево, идеально сбалансированное дерево и дерево, сбалансированное по АВЛ, изучить управление таким деревом, анализ алгоритмов управления.

При выполнении индивидуального задания придерживаться следующей последовательности действий:

изучить словесную постановку задачи;
разработать программу, решающую поставленную задачу;
оттестировать и отладить программу;
написать и представить к защите отчет по работе.

5. Содержание отчета

Титульный лист.
Словесная постановка задачи.
Описание алгоритма восстановления сбалансированности дерева.
Листинг программы, работающей со сбалансированным деревом.
Ответы на контрольные вопросы по согласованию с преподавателем.

6. Варианты индивидуальных заданий

В этой лабораторной работе задание одно общее для всех.

Требуется организовать хранение сбалансированного дерева в памяти ЭВМ, а также реализовать основные операции над сбалансированным деревом: поиск/добавление/удаление.